Black-Scholes Model
The Black-Scholes model, introduced in 1973 by Fischer Black and Myron Scholes, is a fundamental tool in finance for valuing European-style stock options (only actionable at expiry). By considering factors like the current stock price, option strike price, time until expiration, and volatility, the model calculates a theoretical price for options. This standardized approach revolutionized options pricing, enhancing market transparency, facilitating risk management strategies, and fostering financial innovation worldwide.
The Black-Scholes formula:
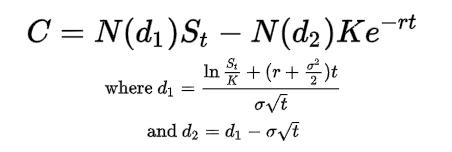
- C: Call option price
- S: Current stock price
- K: Strike price
- t: Time to expiration
- σ: Volatility
- r: Risk-free interest rate
- N: Cumulative distribution function of the standard normal distribution
- d1: "delta" sensitivity of an option's price to changes in the price of the underlying asset
- d2: Rate of change in an option's price relative to changes in the price of the underlying asset
It is used to calculate a "fair" price (where probability of profit and loss are equal), by subtracting the net present value (NPV) of the strike price multiplied by the cumulative standard normal distribution from the product of the stock price and the cumulative standard normal probability distribution function. The model prices options by assuming the underlying asset follows geometric Brownian motion, where its price changes randomly with a drift (expected return) and volatility.